Le divisioni dei polinomi con EDICO

La divisione dei polinomi è un’operazione comune in algebra. In questo tutorial, spiegheremo come dividere i polinomi utilizzando EDICO.

Esempio: $(x^4 + 3x^2 - 4) ÷ (x^2 - 4)$

Per prima cosa identifico i due polinomi, $P(x)$ e $D(x)$, cioé il dividendo e il divisore e li scrivo. La divisione produce due risultati: un quoziente $Q(x)$ e un resto $R(x)$.

1. Definizione dei polinomi:

Vado a scrivere questi polinomi in EDICO, normalmente, senza usare la struttura didattica dove:

• $P(x)$: Questo è il polinomio dividendo. Nel nostro esempio, $P(x) = x^4 + 3x^2 - 4$ è il polinomio che vogliamo dividere.

• $D(x)$: Questo è il polinomio divisore. Nel nostro esempio, $D(x) = x^2 - 4$ è il polinomio con il quale stiamo dividendo $P(x)$.

• $Q(x)$: Questo è il quoziente. Durante la divisione, otteniamo un risultato che chiamiamo $Q(x)$, che rappresenta quante volte il polinomio divisore $D(x)$ si adatta al polinomio dividendo $P(x)$.

• $R(x)$: Questo è il resto. Dopo aver ottenuto il quoziente, può esserci un residuo che non può essere ulteriormente diviso per il polinomio divisore. Questo residuo è chiamato $R(x)$.

e quindi scriverò:

$P(x) = x^4 + 3x^2 - 4$

$D(x) = x^2 - 4$

$Q(x) = ?$

$R(x) = ?$

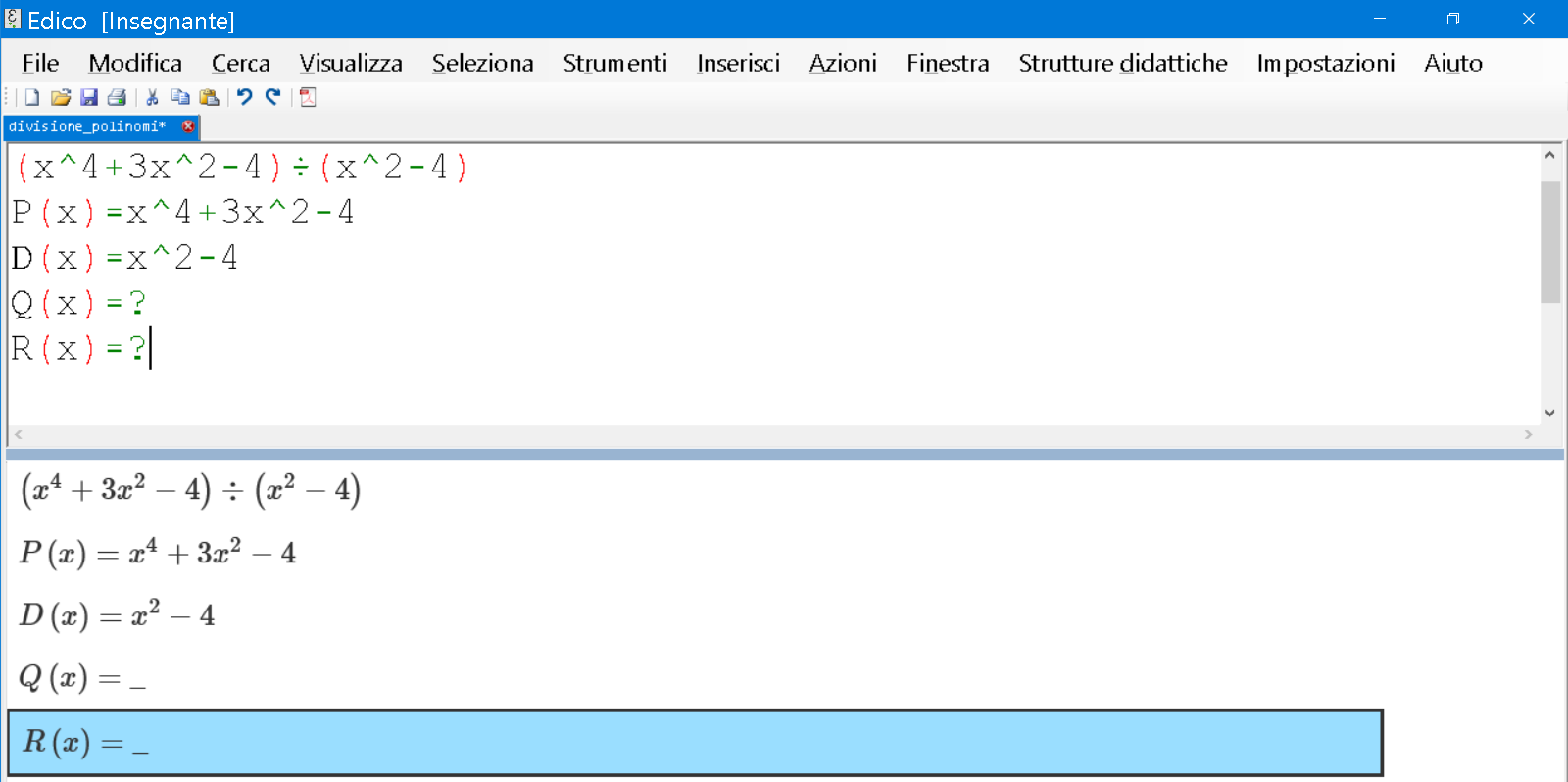
Quindi dobbiamo dividere $P(x)$ per $D(x)$.

Assicuriamoci che entrambi i polinomi siano ordinati in ordine decrescente delle potenze. Completiamo aggiungendo $+0x^3$ e $+0x$, dato che manca il fattore di primo grado. Quindi riscrivo la mia operazione, la seleziono, e dopo averlo fatto dal menu Strutture didattiche scelgo Divisione di polinomi:

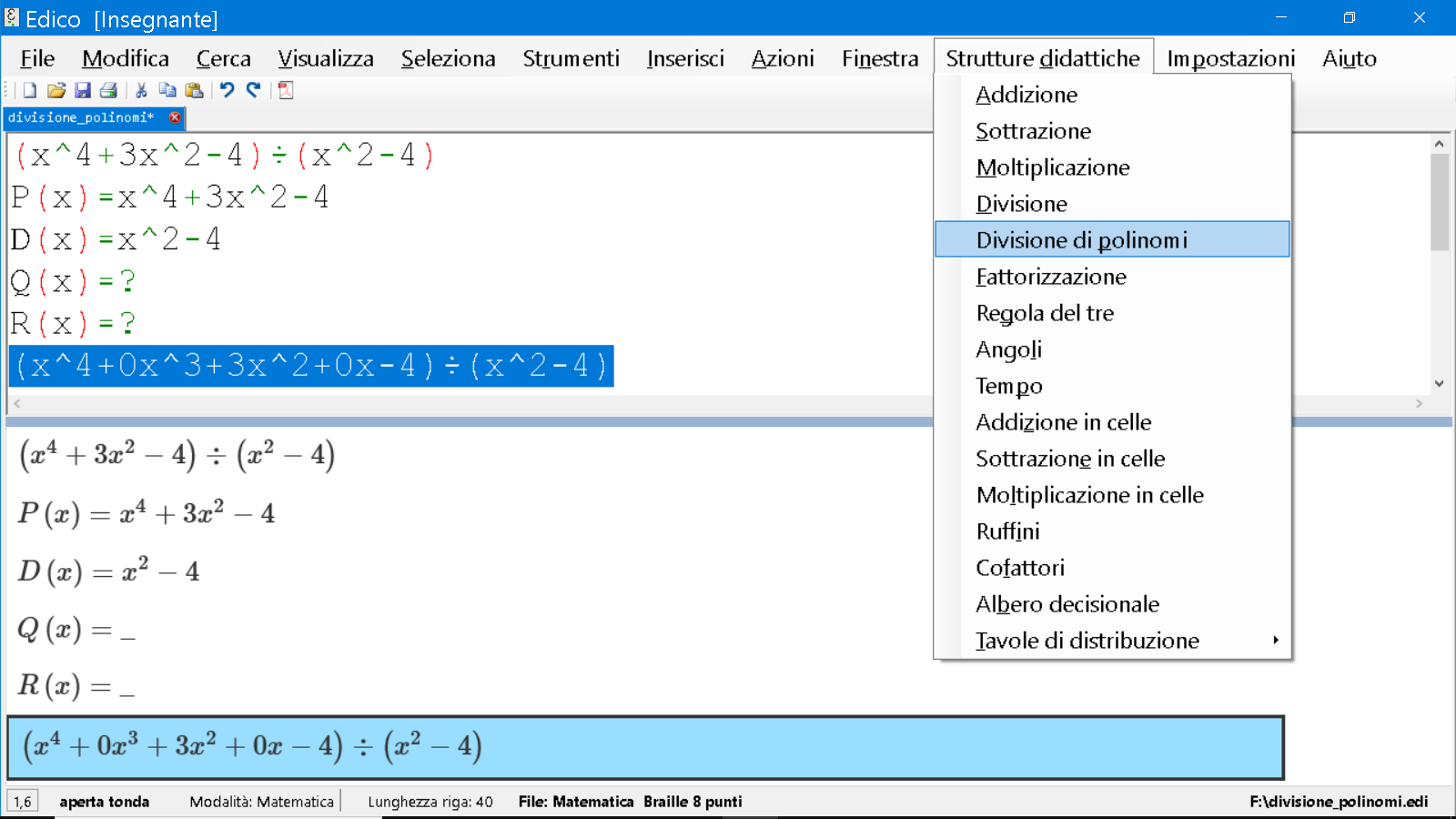
Mi comparirà una schermata, nella quale troverò la mia operazione già impostata con, nella prima riga il dividendo ($P(x)$) il simbolo di divisione e il divisore ($D(x)$)

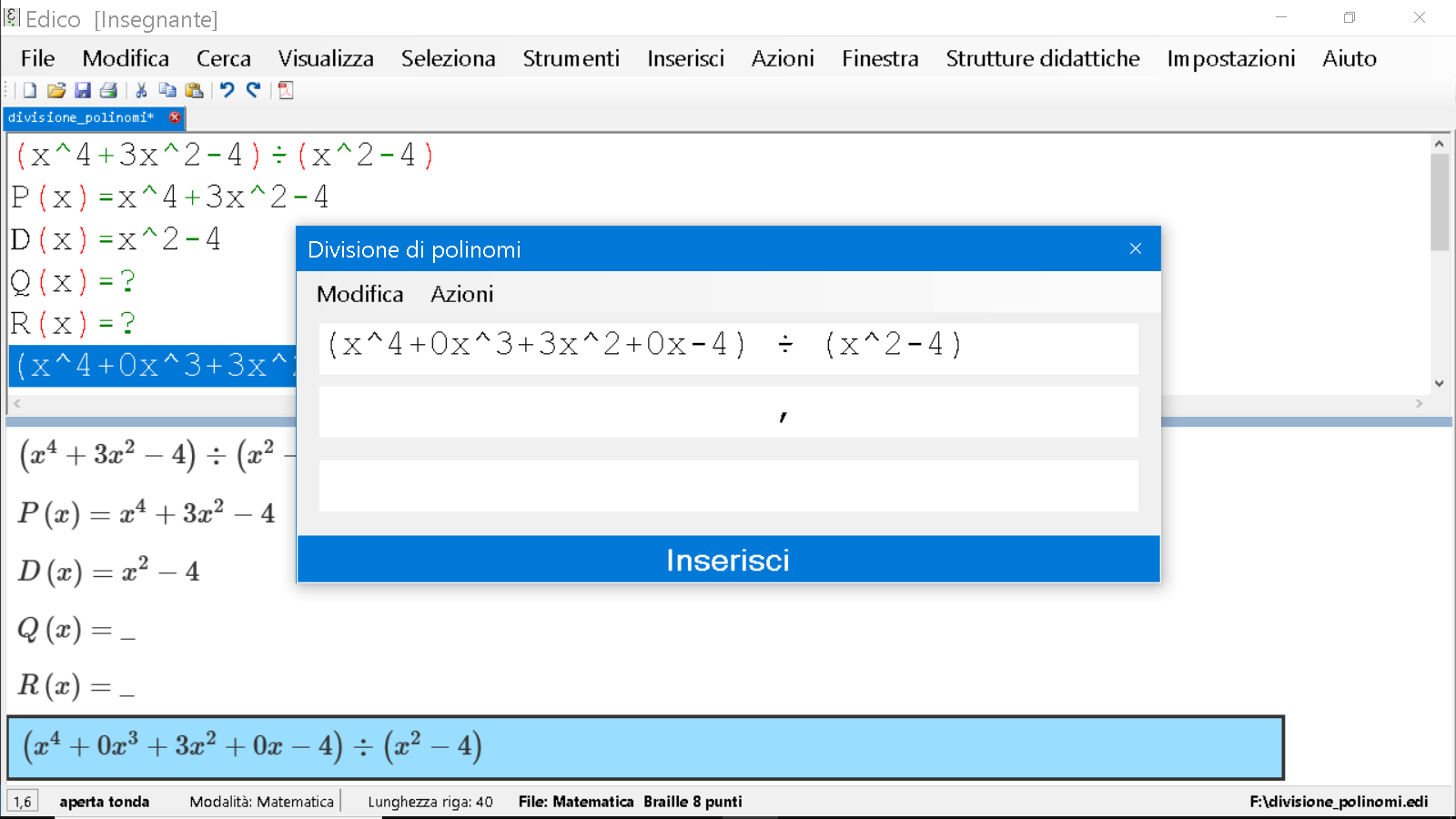
2. Divide il termine di grado più alto di $P(x)$ per il termine di grado più alto di $D(x)$

Dividiamo $x^4$ per $x^2$, i termini di grado più alto dei due polinomi, ottenendo $x^2$. Lo riportiamo sotto, in seconda riga, seconda colonna.

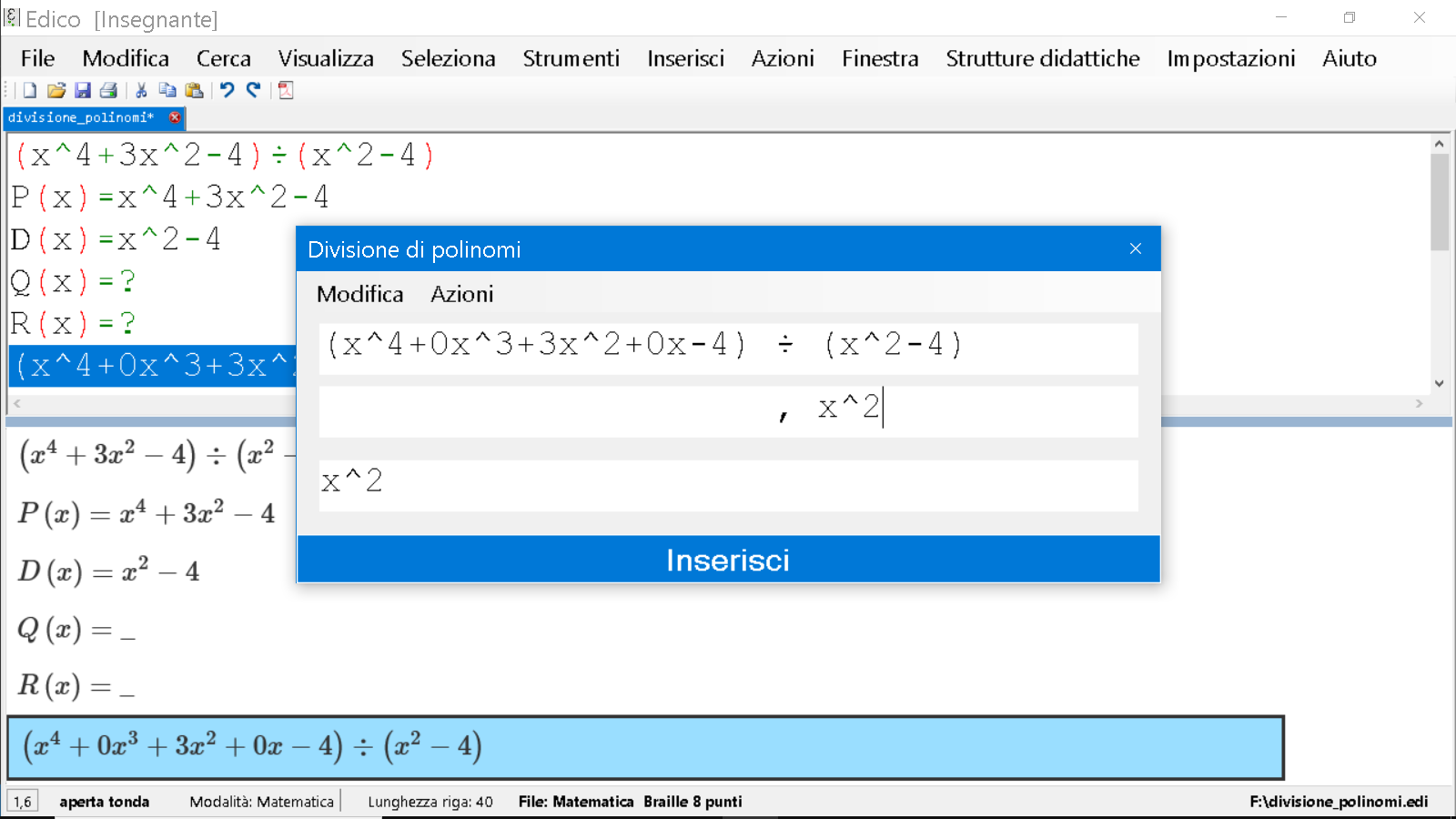
Noto che in ultima riga il programma si preoccupa di riportarmi lo stesso numero, non me ne preoccupo per ora.

3. Moltiplica il risultato per $D(x)$ e sottrai da $P(x)$

Moltiplichiamo $x^2$ per $D(x)$ e sottraiamo il risultato da $P(x)$ (cambiamo di segno e facciamo la somma).

• Quindi quanto fa $x^2 \cdot (x^2-4) $ ? Facciamo i conti e fa $x^4-4x^2 $
• Lo cambiamo di segno e diventa $ -x^4+4x^2 $

Lo riportiamo nella seconda riga, prima colonna (resto):

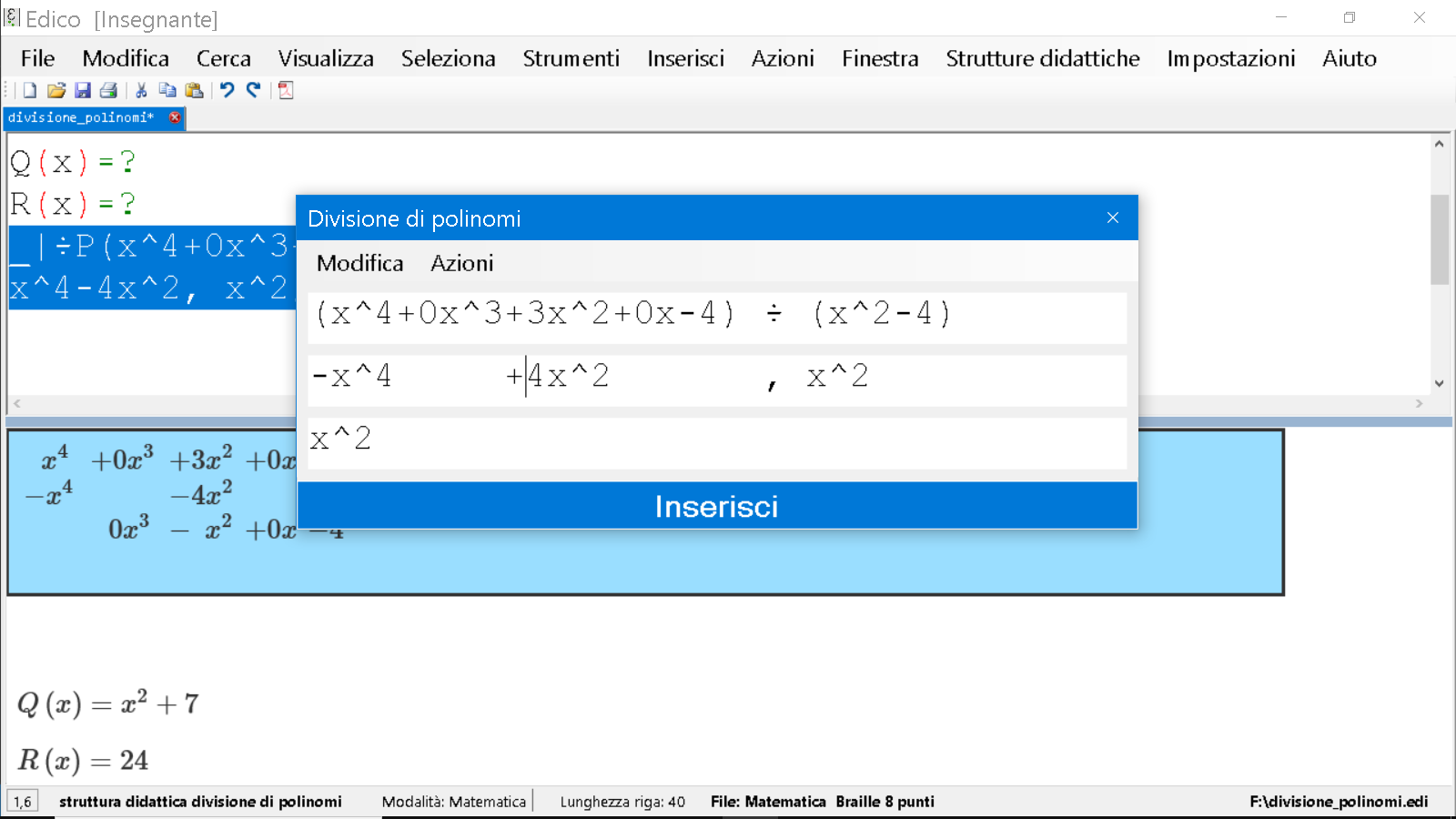
Aggiungiamo una riga, dal menu Modifica, Aggiungi riga o premendo CTRL+N. 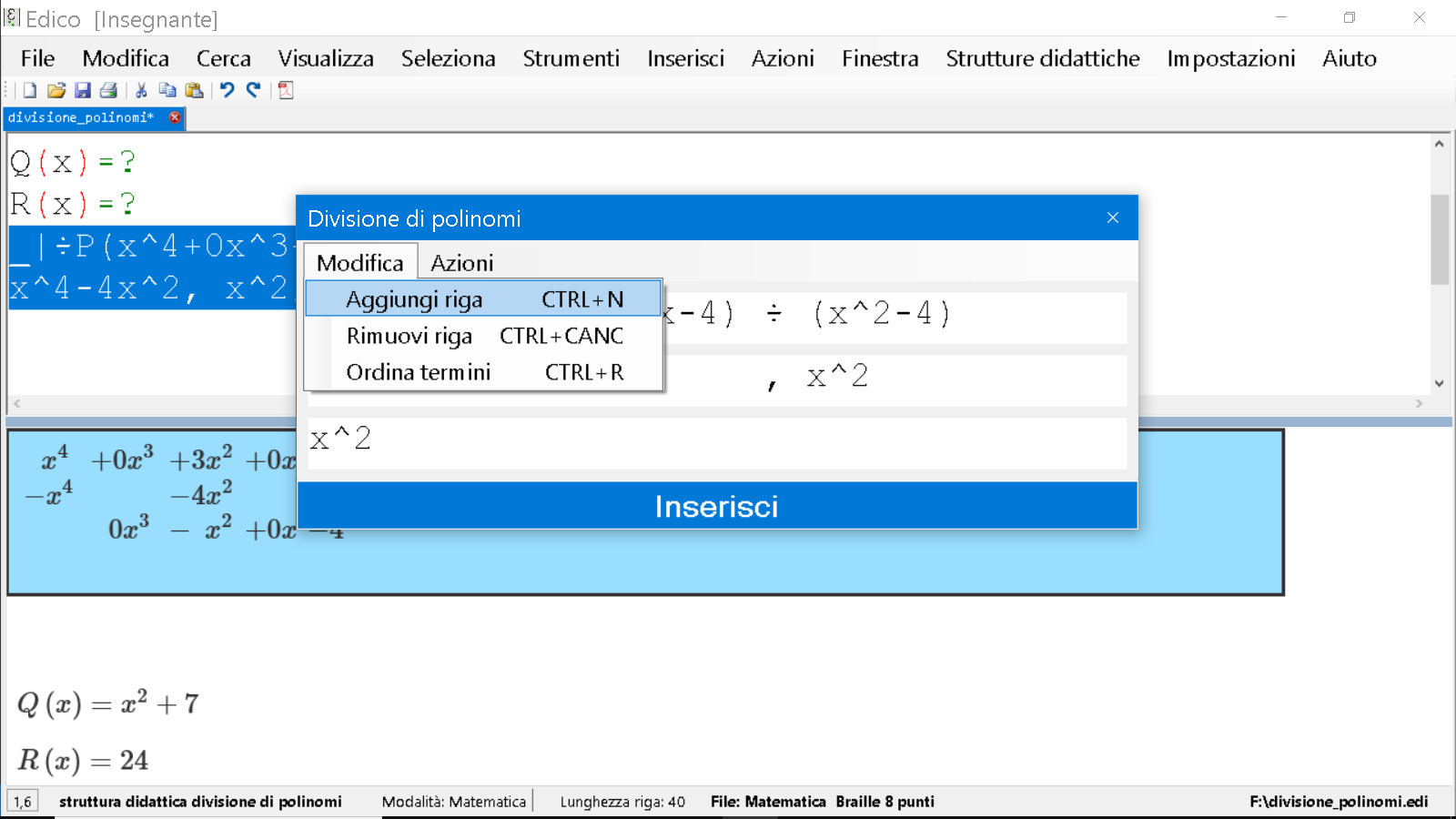Calcoliamo il resto facendo le somme:

4. Ripeti il processo

Aggiungiamo una riga, dal menu Modifica, Aggiungi riga o premendo CTRL+N. Continua il processo finché il grado del resto è inferiore al grado di $D(x)$. Ricordiamoci sempre di andare ad aggiungere i vari termini del quoziente in seconda colonna.

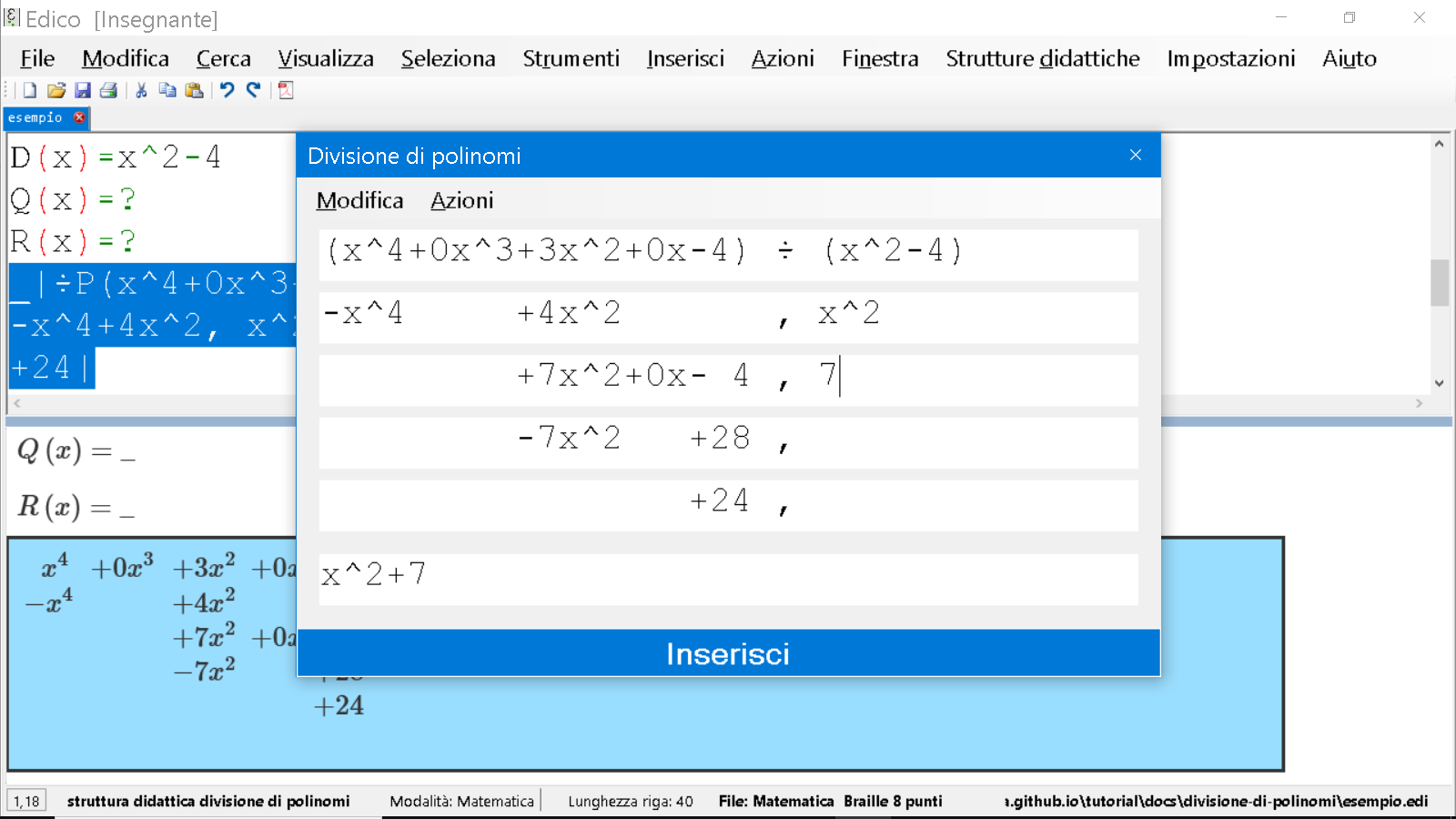
Dal menu Azioni è possibile spostarsi velocemente al Quoziente, all’ultima riga del resto e al risultato.

Notiamo anche che mano a mano che aggiungiamo quozienti nei vari passaggi, questi vengono automaticamente sommati nell’ultima riga (di risultato). Questo evita all’utente di doversi continuamente spostare nella prima riga per accodare i quozienti manualmente.

Quando abbiamo terminato, scegliamo Inserisci o battiamo INVIO .

5. Scrivi il risultato finale

Il risultato della divisione, riportato in ultima riga, è $Q(x) = x^2 + 7$.

Il resto è ciò che è riportato nella penultima riga, $R(x) = 24$.

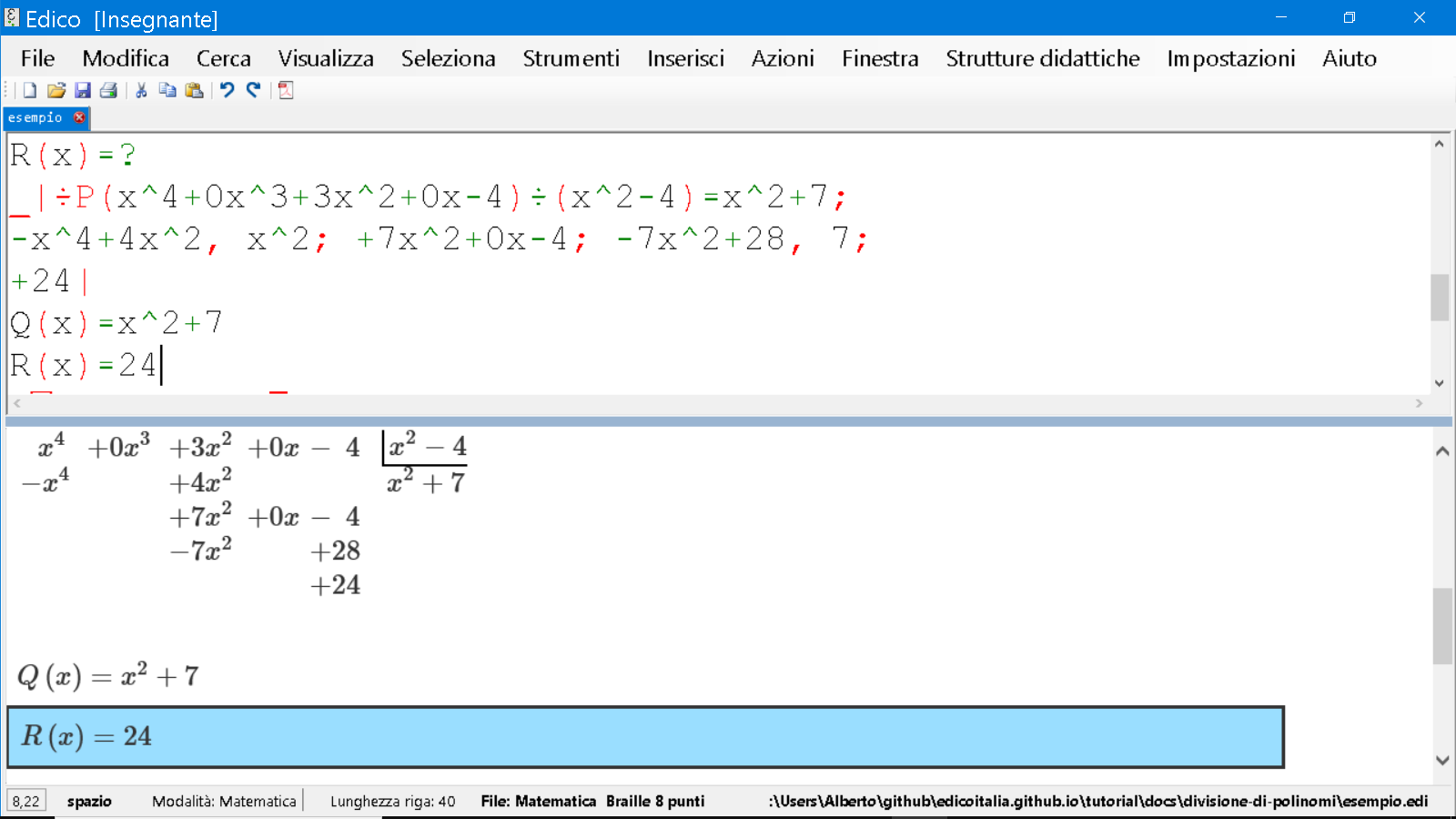
Verifica:

Sapendo quindi che $P(x) = D(x) \cdot Q(x) + R(x)$ , possiamo fare la verifica.

$P\left(x\right)\;=\;D\left(x\right)\cdot Q\left(x\right)\;+\;R\left(x\right)$

$P\left(x\right)\;=\;\left(x^{2}-4\right)\cdot \left(x^{2}+7\right)\;+\;24\;\;$

$P\left(x\right)\;=\;\left(x^{4}-4x^{2}+7x^{2}-28\right)\;+\;24$

$P\left(x\right)\;=\;\left(x^{4}+3x^{2}-28\right)\;+\;24$

$P\left(x\right)\;=\;x^{4}+3x^{2}-4$

Il $P(x)$ trovato corrisponde al nostro polinomio di partenza, Verificato.

Allegati

Gli esempi di questo tutorial sono disponibili già completati a questo link